ANGULOS EN LA CIRCUNFERENCIA

ANGULOS EN LA CIRCUNFERENCIA

Los ángulos en una circunferencia pueden ser

ANGULO CENTRAL, si tiene su vértice en el centro de esta. Sus lados son dos radios.

ANGULO INSCRITO , si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.

ANGULO SEMI-INSCRITO, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.

ANGULO INTERIOR , si su vértice está en el interior de la circunferencia.

ANGULO EXTERIOR, si tiene su vértice en el exterior de la circunferencia y sus lados son rectas secantes o tangentes a ella.

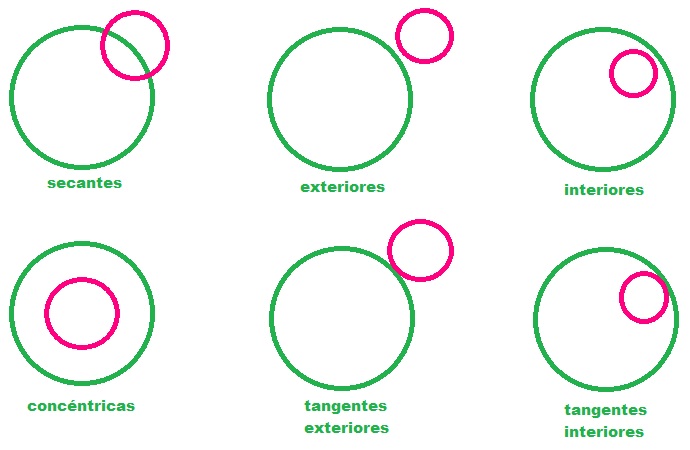
LAS POSICIONES DE DOS CIRCUNFERENCIAS pueden ser:

EXTERIORES, si no tienen puntos comunes y los puntos de una de ellas son exteriores a la otra circunferencia. No importa que tengan igual o distinto radio. 

TANGENTES EXTERIORMENTE, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. No importa que tengan igual o distinto radio. 

SECANTES, si se cortan en dos puntos distintos. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos.

TANGENTES INTERIORMENTE, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra exclusivamente. Una de ellas tiene que tener mayor radio que la otra. 

CONCENTRICAS, si tienen el mismo centro  y distinto radio. Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra. 

INTERIORES EXCENTRICAS, si tienen diferente centro y no tienen punto común. Una de ellas tiene que tener mayor radio que la otra.

COINCIDENTES, si tienen el mismo centro y el mismo radio. Si dos circunferencias tienen más de dos puntos comunes, necesariamente son circunferencias coincidentes.

EJERCICIO: Use regla, compás y transportador para dibujar

1.  En circunferencias de radios 3, 4 y 5 cm dibujar respectivamente ángulos centrales de 60°, 125° y 225°

2.  En circunferencias de radios 3, 4 y 5 cm dibujar respectivamente ángulos inscritos de 90°, 70° y 40°

3.  En circunferencias de radios 4 y 5 cm dibujar respectivamente ángulos interiores de 65° y 120°

4.  En circunferencias de radios 3 y 4, cm dibujar respectivamente ángulos semi-inscritos de 60° y 90° 

5.  En circunferencias de radios 3,5 y 4,5 cm dibujar respectivamente ángulos exteriores de 40°  y 65° 

 

6.  Dibujar 4 circunferencias tangentes interiores, 3 concéntricas, 4 secantes y 4 tangentes exteriores.   

OPERACIONES COMBINADAS

OPERACIONES COMBINADAS

OBSERVA Y ANALIZA LOS EJEMPLOS DE LA SIGUIENTE PRESENTACION :
http://contenidosdigitales.ulp.edu.ar/exe/matematica1/operaciones_combinadas_con_nmeros_enteros.html 

COPIA LOS 2 EJEMPLOS  QUE HAY AL FINAL DE LA PRESENTACION

JERARQUIA DE LAS OPERACIONES.

Se realizan las operaciones indicadas siempre en el siguiente orden:

1º. Efectuar las operaciones entre paréntesis, corchetes y llaves.                                     

2º. Calcular las potencias y raíces.                                                                                    

3º. Efectuar los productos, cocientes.                                                                                
4º. Realizar las sumas y restas. 

EJEMPLOS de Operaciones combinadas

1.  SIN PARENTESIS:

a)  Sumas y diferencias.                                                                                                     

9 − 7 + 5 + 2 − 6 + 8 − 4 = 24 - 17 = 7

b)  Sumas, restas y productos.                                                                                          

3 · 2 − 5 + 4 · 3 − 8 + 5 · 2 =                                                                            

Realizamos primero los productos por tener mayor prioridad                                 

6 − 5 + 12 − 8 + 10 =

Efectuamos las sumas y restas.

= 28 − 13 = 15                                                                                                                

c)  Sumas, restas , productos y divisiones.

10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 2 − 16 : 4 =

Realizamos los productos y cocientes en el orden en el que los encontramos porque las dos operaciones tienen la misma prioridad.

= 5 + 15 + 4 − 10 − 8 + 8 − 4 =

Cancelamos opuestos y efectuamos las sumas y restas.

= 32 − 22 = 10                                                                                                               

d)  Sumas, restas , productos , divisiones y potencias.

2³ + 10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 2² − 16 : 4 =

Realizamos en primer lugar las potencias por tener mayor prioridad.

= 8 + 10 : 2 + 5 · 3 + 4 − 5 · 2 − 8 + 4 · 4 − 16 : 4 =

Seguimos con los productos y cocientes.

= 8 + 5 + 15 + 4 − 10 − 8 + 16 − 4 = 26
 

 2.  CON PARENTESIS

(15 − 4) + 3 − (12 − 5 · 2) + (5 + 16 : 4) −5 + (10 − 2³)=

Realizamos en primer lugar las operaciones contenidas en ellos.

= (15 − 4) + 3 − (12 − 10) + (5 + 4) − 5 + (10 − 8 )=

Quitamos paréntesis realizando las operaciones.

= 11 + 3 − 2 + 9 − 5 + 2 = 18  

 

3.  CON PARENTESIS Y CORCHETES

[15 − (2³ − 10 : 2 )] · [5 + (3 ·2 − 4 )] − 3 + (8 − 2 · 3 ) =

Primero operamos con las potencias, productos y cocientes de los paréntesis.

= [15 − (8 − 5 )] · [5 + (6 − 4 )] − 3 + (8 − 6 ) =

Realizamos las sumas y restas de los paréntesis.

= [15 − 3] · [5 + 2 ] − 3 + 2=

En vez de poner corchetes pondremos paréntesis directamente:

= (15 − 3) · (5 + 2) − 3 + 2=

Operamos en los paréntesis.

= 12 · 7 − 3 + 2

Multiplicamos.

= 84 − 3 + 2 = 83

4.  OTROS EJEMPLOS:

a)  4 − 3.(4 − 3) + 2.(− 9 + 5) 

= 4 - 3.(1) + 2(- 4) = 4 -3 -8 = -7                     

b)  2³ - 5 - 4.( 2 - 6) 

= 8 - 5 - 4.(- 4) = 8 -5 + 16 = 19                                    

c)  -20:5 + 2.(- 8 + 12: -4) 

= - 4 + 2.(- 8 - 3) = - 4 + 2.(-11) = - 4 - 22 = - 26

REPASA LA JERARQUIA DE LAS OPERACIONES OBSERVANDO LOS EJEMPLOS DE LOS SIGUIENTES VIDEOS:

https://youtu.be/P6mBE-1oXQM 

https://youtu.be/yxKsUpjbWY8 

 

EJERCICIO: 

1. Resuelve teniendo en cuenta la jerarquía de las operaciones   

  

e)  36: (- 9) - 4.(3 - 7) =

f)  2 - 5.8 + 6 :( -3) - 7.(5 - 2)

g)  -7 - 4.(- 3) +16:( - 2)

h)  10 - 9.(- 3) + 4

i)  15 -3.(9) + 5.(-6) - 24:(-8)

                                                                    

 

ROPIEDADES DE LA RADICACION

PROPIEDADES DE LA RADICACION.

OBSERVA Y ANALIZA LAS PROPIEDADES DE LA RADICACION EN EL SIGUIENTE VIDEO: https://youtu.be/Qaw-cB3LBdY

 

La radicación es en realidad otra forma de expresar una potenciación: la raíz de cierto orden de un número es equivalente a elevar dicho número a la potencia inversa. Por esto, las propiedades de la potenciación se cumplen también con la radicación. Para que estas propiedades se cumplan, se exige que el radicando de las raíces sea positivo.

Raíz de un producto

La raíz de un producto es igual al producto de las raíces de los factores:

Ejemplo

•  =  = 

Se llega a igual resultado de la siguiente manera:

Raíz de un cociente

La raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador:

Ejemplo

• 

Raíz de una raíz

Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva el radicando:

Ejemplo

•  =    Es inexacta por que no hay ningun entero que elevado a la 27 de 5 
•  
•  EJERCICIOS: RESOLVER.
• 1)   
• 2)    
• 3)    
• 4)   
• 5)    

• 6)  Exprese como raices y resuelva:
• a)  Raiz cuadrada de 36 menos raiz cubica de 125
• b)  Raiz cuarta de 16 menos raiz quinta de - 32 
• c)  Raiz cúbica de - 27 más raiz cuadrada de 64
• d)  Raiz cúbica de 125 menos raiz cuadrada de 81                                                            

RADICACION DE NÚMEROS ENTEROS.

RADICACION DE NÚMEROS ENTEROS.

LA RADICACION es la operacion inversa de la POTENCIACION y la utilizamos para hallar LA BASE DESCONOCIDA, ASÍ:

La radicación es la operación que “deshace” la potenciación.

Porque (3)² = 9.
En el ejemplo anterior, el 9 se llama radicando, el 2 índice y el resultado 3, raíz.
La definición formal de esta operación es la siguiente:

Si n es un número natural, se dice que el número entero a es la raíz enésima del número entero b, si b es la potencia enésima de a. Es decir:
 
n se llama INDICE  y es el valor del EXPONENTE en la POTENCIACION.
b se llama RADICANDO y es el resultado de la POTENCIACION.
a se llama RAIZ y es BASE en la POTENCIACION.
Si en la RADICACION no aparece el INDICE, colocamos el 2 y leemos RAIZ CUADRADA.
 
Veamos otros ejemplos:
 
  Veamos que sucede cuando el radicando es un número negativo:
 
En el ultimo ejemplo se debería buscar un número elevado "a la cuatro" que de como resultado -81, ¿existirá algún número que cumpla esa condición?
Si recordaste lo estudiado cuando se trabajó con la operación de potenciación, tu respuesta debería ser negativa, no existe ningún número entero que cumpla esa condición (Recuedrde que todo número con exponente PAR da +). 
En general: cuando el índice es par y el radicando un número negativo, el resultado no existe en el conjunto de los números enteros.

LA RADICACION NO ES UNA OPERACION INTERNA EN LOS ENTEROS POR QUE HAY RAICES QUE SON INEXACTAS (NUMEROS DECIMALES) 


RAIZ CUADRADA EXACTA DE UN ENTERO

La raíz cuadrada de un número entero positivo es el valor positivo que elevado al cuadrado es igual a dicho número.

Ejemplo:

El radicando es siempre un número positivo o igual a cero, ya que todo número al cuadrado es positivo.

Ejemplo:

 

porque ningún entero elevado al cuadrado es negativo, siempre es positivo.

Las raíces cuadradas de números enteros tienen dos signos: positivo y negativo.

Ejemplo:

La raíz cuadrada es exacta, siempre que el radicando sea un cuadrado perfecto.

     

RAICES POR DESCOMPOSICION DEL RADICANDO EN FACTORES PRIMOS.

 

OBSERVA EL PROCEDIMIENTO EN EL SIGUIENTE VIDEO https://youtu.be/uUPHpMHtfXY

 

 

EJERCICIO: Simbolizar las siguientes raices y resolverlas descomponiendo en factores primos:

 

a)  Raiz cuadrada de 81

b)  Raiz cúbica de 64

c)  Raiz quinta de 243

d)  Raiz cuadrada 900

e)  Raiz cúbica de 216

f)  Raiz cuadrada de 324

g)  Raiz cuadrada de 2025

h)  Raiz cúbica de 1728

i)  Raiz cuarta de 1296

j) Raiz cuadrada de 2500