LONGITUD DE LA CIRCUNFERENCIA Y EL AREA DEL CIRCULO.

NOTA: COPIAR CONCEPTOS Y EJEMPLOS EN EL CUADERNO DE GEOMETRÍA, PARA LA PROXIMA SEMANA. LOS EJERCICIOS LOS DESARROLLAMOS EN LA CLASE.

1.- LONGITUD DE LA CIRCUNFERENCIA.

EJEMPLO 1. Vamos a calcular la longitud de esta circunferencia conocido el diámetro:

 Longitud de la circunferencia = 3 x 3,14 = 9,42 m

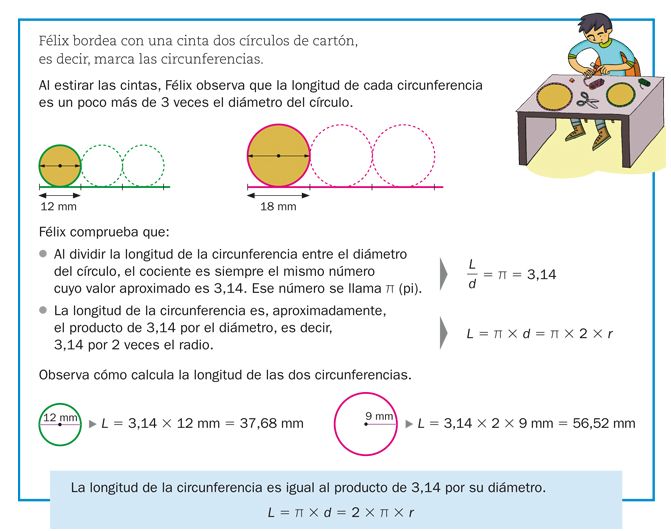
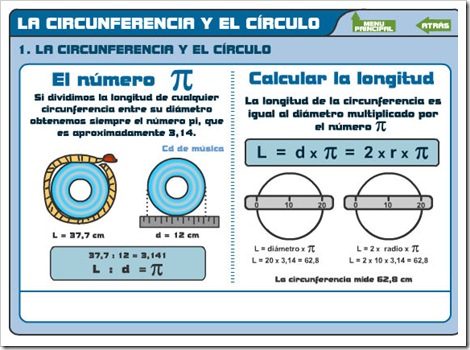
EJEMPLO 2. Vamos a calcular la longitud de esta circunferencia conocido el radio:

En este ejemplo conocemos la longitud del radio y el diámetros es 2 veces el radio ( 2.r ), entonces,

Longitud de la circunferencia = 2 x 2 x 3,14 = 12,56 m

  
2.- AREA DEL CIRCULO.

 

EJEMPLO 3. Vamos a calcular el área de este círculo:

 

Área del círculo = 3 x 3 x 3,14 = 28,26 m2
  
EJEMPLO 4. Vamos a calcular el área de este círculo de diámetro 10 metros:
Entones el radio mide 5 metros. ( el radio es la mitad del diámetro)

Área del círculo = 5 x 5 x 3,14 = 78,50 m2

En el siguiente video observarás ejemplos de longitud de la circunferencia y área del círculo:
https://youtu.be/3mLIsSiichQ 

EJERCICIOS: Resolver copiando cada enunciado y la solución respectiva.



4.-  Calcula la longitud de media circunferencia de radio 200 cm.

5.-  Calcula el área de un círculo cuyo radio mide 7 cm.

6.-  a)  Cuántos metros avanza una rueda de 45 cm de radio cuando da 25 vueltas en línea recta?
      b)  Las llantas de una bicicleta tienen radios de 40 cm y recorren una distancia de 15.072 cm, cuántas vueltas dió cada llanta?

7.-  Un parque de forma circular con un diámetro de 80 metros tiene en el centro una fuente circular de radio 5 metros.

a)  Hacer un dibujo representativo del parque.
b) Al parque y a la fuente los rodea una reja respectivamente. Cuál es la longitud de la reja del parque y de la reja de la fuente?
c)  Cuál es el área del parque?
d)  Cuál es el área de la fuente)
e)  Entre la circunferencia del parque y la circunferencia de la fuente está el área de paseo y juegos. Cuál es esta área?

8.-  En una esquina de un lote rectángular come pasto un caballo, el cual esta amarrado con un lazo de 6  metros.

a)  Que área del lote puede pastar el caballo?
b)  Cuál es el perímetro de esta área?

9.-  Calcular el área de cada círculo y su perímetro con un  
a)  Diámetro de 30 cm.
b)  Diámetro de 50 cm.

10.-  Halle el radio y el diámetro de las circunferencias cuyas longitudes son:
a)  314 cm
b)  628 cm
c)  2512 cm

11.-  Halle el radio de los círculos cuyas áreas son:
a)  78,5 cm2
b)  314 m2
c)  200,96 cm2 

FRACCIONES EQUIVALENTES.

FRACCIONES EQUIVALENTES:
Son aquellas que representan lo mismo.

                                                           

 Si al rectángulo anterior se lo divide en 8 partes iguales y se pintan 6, se obtiene la siguiente representación.

Observando ambas representaciones resulta que la parte sombreada es la misma:

Entonces,   pues representan la misma parte sombreada. Estas fracciones se denominan equivalentes.

Una manera de encontrar fracciones equivalentes de una fracción dada es multiplicar o dividir (si es posible) numerador y denominador por un mismo número, distinto de cero.

En el caso anterior se multiplica numerador y denominador por 2, es decir:  

La acción de multiplicar numerador y denominador por un mismo número, para hallar fracciones equivalentes se denomina AMPLIFICAR y por otro lado si se buscan fracciones equivalentes dividiendo numerador y denominador por un mismo número, sí es posible, se llama SIMPLIFICAR. 

REFUERZA este concepto en el siguiente video: https://youtu.be/mBCBu4fpH20

La fracción que no se puede simplificar se llama FRACCION IRREDUCIBLE.


El proceso de obtener 1/2 = 2/4 = 4/8 = 3/6 = ... es infinito y se llama AMPLIFICAR.
El proceso de obtener 4/8 = 2/4 = 1/2 es finito y se llama SIMPLIFICAR.
Se observa que las fracciones anteriores representan lo mismo (la mitad), son equivalentes.

EJEMPLOS:
1.  AMPLIFICAR 2/5. 
Multiplicamos numerador y denominador por un mismo número obteniendo fracciones equivalentes. este proceso es infinito, así:
2/5 = 2x2/5x2 = 4/10 = 2x3/5x3 = 6/15 = 2x6/5x6 = 12/30 y así sucesivamente, todas las veces qque queramos.
Entonces: 2/5 = 4/10 = 6/15 = 12/30 = ...
También observamos que 2/5 = 4/10 son equivalentes porque el producto en cruz es igual, así:
2x10 = 5x4 = 20

Pero 3/4 NO ES EQUIVALENTE CON 18/20 PORQUE 3X2O = 60 Y 4X18 = 72


2.  SIMPLIFICAR 45/60 HASTA OBTENER UNA FRACCION IRREDUCIBLE.
Dividimos cada que sea posible numerador y denominador por un mismo número (DIVISOR COMUN). Este proceso es finito. Así:
45/60 = 45:5/60:5 = 9/12 = 9:3/12:3 = 3/4 y no podemos dividir mas.
Entonces 45/60 = 9/12 = 3/4 y 3/4 es la fracción irreducible.

EJERCICIO 1: Complete el espacio con un número para que las fracciones sean equivalentes, pase de la fracción completa a la fracción con el espacio y diga si usó amplificación o simplificación, además comprueba en cada caso que el producto cruzado es igual. 

Ejemplo: __/8 = 15/24, entonces 15/24 = 15:3/24:3 = 5/8, entonces 5/8 = 15/24 
porque 5x24 = 8x15 = 120. Proceso: SIMPLIFICACION.
    
 
EJERCICIO 2: AMPLIFICAR cada fracción 5 veces. Cada vez indique el amplificador.
Ejemplo:
 
Encuentre el error  en el ejemplo anterior y corríjalo.

a) 4/3      b) 5/9      c) 1/6      d) 8/3      e) 10/7

EJERCICIO 3: SIMPLIFICAR cada fracción hasta la fracción irreducible. Indique el simplificador cada vez.
Ejemplos:
 


a) 42/36      b) 15/9      c) 81/63      d) 8/32      e) 10/70      f) 125/100      g)  105/72

EJERCICIO 4: SIMPLIFICAR
   

LOS NUMEROS RACIONALES.

LOS NUMEROS RACIONALES.
INTRODUCCION.

OBSERVE CON ATENCION los siguientes videos:
VIDEO 1: https://youtu.be/vvsdX1H3Ujk 

VIDEO 2: https://youtu.be/M6xKMgfp8aU 

 

Seguramente más de una vez has visto en los medios de comunicación, en los negocios o hablando con algún amigo expresiones de este tipo:
• Un cuarto kilogramo de pan: 1/4.
• Compramos una gaseosa de un litro y medio: 1 1/2 = 3/2.
• Siete de los 20 alumnos de un curso no aprobaron Matemática: 7/20.
• Se quiere repartir 8 porciones de pizza entre 5 amigos: 8/5.
Todas estas formas de hablar se representan en matemáticas por un tipo de números que se llaman fracciones.
Comenzaremos definiendo matemáticamente qué es una fracción:
 
Los números enteros y las fracciones forman el conjunto de los Números Racionales. Este conjunto se denota con la letra Q.
Las características que tienen los números Racionales son:

• Es un conjunto infinito.
• Entre dos números racionales existe siempre infinitos números racionales, por tal motivo se dice que este conjunto es denso. 
• No tiene ni primer ni último elemento. 

RECUERDE: LA DIVISION EN LOS ENTEROS NO ES UNA OPERACION INTERNA, por que hay divisiones inexactas y su resultado son números decimales los cuales no pertenecen a los ENTEROS. Estas divisiones se dejan indicadas como fracciones, a:b = a/b, así 2:3 = 2/3  
 
De la misma forma como la sustracción nos condujo a considerar números negativos, la división de dos números  naturales o enteros no siempre es un elemento de IN o de ZZ , lo que nos motiva a extender estos conjuntos a un conjunto denominado “Conjunto de los Números Racionales” denotado por Q. Los elementos de este conjunto Q,  llamados números racionales son entonces de la forma: 

a/b, donde  a y b son enteros  y  b diferente de 0.                                                                                             
En general el conjunto Q, se define como: Q = { a/b, / a y b son enteros y b es distinto de 0} 
 

Si la fracción a/b indica una división exacta, representaría un número entero, por lo tanto TODO NUMERO ENTERO ES UN NUMERO RACIONAL, así 6/2 = 3 ó - 10/2 = - 5

REPRESENTACION GRAFICA DE FRACCIONES.
OBSERVA EL SIGUIENTE VIDEO:
VIDEO 3: https://youtu.be/Hl7mx-XtPl8

Si representas un número racional  como una fracción , el número   a se llama  numerador y  b  denominador .
El denominador de una fracción indica la cantidad de partes iguales en que se debe dividir la unidad, y el numerador indica cuántas de esas partes se deben tomar. En el siguiente ejemplo se dividió en cuatro un rectángulo y se pintaron tres de esas partes en que quedó dividido.
Ejemplo:



EJERCICIO 1: Resuelve en tu cuaderno. 
 

REPRESENTACION Y CLASIFICACION DE FRACCIONES:
 
OBSERVA los siguientes videos:
VIDEO 4: https://youtu.be/aWw5FhEvtnQ

VIDEO 5: https://youtu.be/hkA9SIze65M

EJERCICIO 2: Represente gráficamente las siguientes fracciones impropias y páselas a números mixtos.
a) 10/3   b) 15/4   c) 17/6   d) 5/2   d) 19/8   e) 17/5   h) 27/20   i) 19/12

EJERCICIO 3: Represente gráficamente las siguientes fracciones
a) 9/3   b) 4/4   c) 12/6   d) 5/5   d) 6/2   e) 15/5   h) 20/20   i) 16/8
¿Cómo se llaman las anteriores fracciones?

EJERCICIO 4:  Responde en tu cuaderno
a) Que son fracciones propias. Dé 4 ejemplos.
b) Que son fracciones impropias. Dé 4 ejemplos y páselas a número mixto
c) Que son fracciones mixtas. Dé 4 ejemplos y páselas a fracciones impropias.
d) Que son fracciones homogéneas. Dé 4 ejemplos.
e) Que son fracciones heterogéneas. Dé 4 ejemplos.
f) Que son fracciones equivalentes. Dé 4 ejemplos.
g) Pase las siguientes fracciones impropias a números mixtos:


h) Pase los siguientes números mixtos a fracciones impropias: